①ステップ送り
最も簡単なのは，四角形を並べてパターンを作る方法
・四角形に絵を描く
このときのコツは，移動したときに絵柄同士がぶつからないようにすること．
四角形の四辺に接していない部分は，後から書き足してもいい．
②ハーフステップ送り
ステップ送りは簡単だが，単調で，絵柄の境界線が見抜かれやすい，という特徴をもつ．
そこでよく使われるのが，ハーフステップ送り．
ステップ送りよりも絵柄の境界線が目立ちにくい．
同じ距離で水平に並ぶ数が半分になる．
ステップ送り，ハーフステップ送り
タイリング
四角形を並べることができたら，四角形を少し変形しても並べることができることに気付くでしょう．
四角形の一辺を変形．
変形した辺を対辺に移動して，変形した四角形を作る．
これを移動しながら複製．複製した辺同士なので，必ずぴったりはまることがわかります．
同じように，もう縦方向の辺も変形して複製してみると，
ぴったりはまるタイルが繰り返せます．
上の例において，辺の移動のさせ方は，天地：平行移動，左右：平行移動ですが，以下に示すような，その他のやり方でもタイルを作ることができます．
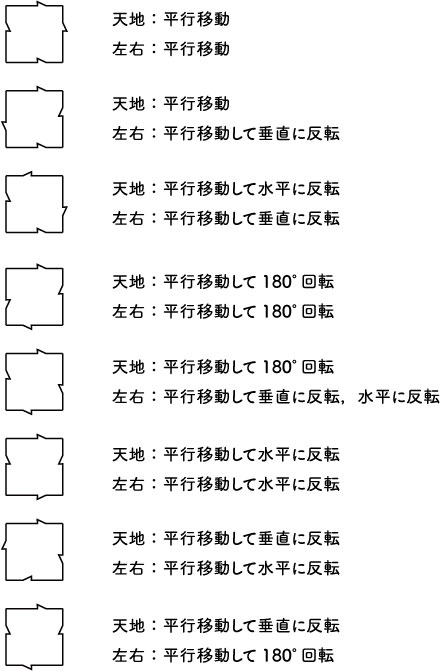
何かに「見立て」をすることで，同じ図形でも全くちがったものに見えることもあります．
M. C. エッシャーによるタイリングは，およそこのような技法によるものです．
また，後年，イソヘドラル・タイリングという名前で93種類が分類されています．
https://www.jaapsch.net/tilings/mclean/html/triangle_templates.html
17種類のウォールペーパーパターン（2） 作例
ここで使うプリミティブ（基本となる1パーツ）
p1
並進のみ．
pm
並進して鏡映．
pg
並進してすべり鏡映．
cm
鏡映して移動するのはpmと同じだが，移動のしかたが異なる．
p2
180°回転して並進．
pmm
鏡映したものをさらに鏡映．
cmm
pmmと同じく鏡映したものを鏡映するが，鏡映軸が異なる．ひし形をイメージするとわかりやすい．
pgg
すべり鏡映してからすべり鏡映．
pmg
鏡映して，すべり鏡映．
p4
4回割り（90°回転）して移動．
p4m
90°回転して鏡映．
p4g
90°回転してすべり鏡映．
p3
3回割り（120°回転）して移動．
p31m
鏡映して120°回転．
p3m1
鏡映して120°回転．（p31mとほとんど同じ．p31mは鏡映軸が回転の中心を通るが，p3m1は回転の中心を通らない鏡映軸がある）
p6
6回割り（60°回転）して移動
p6m
鏡映して60°回転．
非周期的パターン
同じ図形での周期的パターン
同じ図形で平面充填されているが、配置される位置は繰り返しではない。
五角形による非周期パターン
平面充填可能な五角形は15種類あり，これ以上は存在しないとされている．（ここでは１つだけ紹介）
同じ図形ではない非周期的パターン
ペンローズ・タイル
2020年のノーベル物理学賞受賞者，ロジャー・ペンローズ（イギリスの数理物理学者、数学者）が作った，有名な非周期的パターン．
「凧」とよばれるパーツと「矢」とよばれるパーツで構成される．
ペンローズ・タイルにはいくつか種類があるが、ここに紹介するのは「無限の星」とよばれるもの。非周期性のまま，無限に平面充填できる．
正多角形ではない，1種類または2種類の図形による周期的パターン
正多角形を（ほとんど）使わないパターンの紹介
17種類のウォールペーパーパターン（１）概説
周期性のある平面充填のパターンは17種類あり、これ以上存在しないことが証明されている。
https://ja.wikipedia.org/wiki/文様群
4つの基本移動と17の法則の表記法
- 並進
- 鏡映
- 回転
- すべり鏡映
この4つの組み合わせで17種類のバリエーションが生まれる。
それぞれの名称と特徴
pはprimitive（単純格子）、mはmirror（鏡映）、gはglide（すべり鏡映）、cはface centerd（面心格子あるいは有心格子）、数字はn回割り（360°を何回割ったか）を表す。
- （A）回転を含まない。
| p1 | 鏡映、すべり鏡映を含まない。 |
| pm | 鏡映を含む。すべり鏡映軸は必ず鏡映軸でもある。 |
| pg | 鏡映を含まない。すべり鏡映を含む。 |
| cm | 鏡映を含む。鏡映軸ではないすべり鏡映軸がある。 |
- （B）180°回転を含む。90°、60°回転を含まない。
| p2 | 鏡映、すべり鏡映を含まない。 |
| pmm | 鏡映を含む。すべり鏡映軸は必ず鏡映軸でもある。 |
| pgg | 鏡映を含まない。すべり鏡映を含む。 |
| cmm | 鏡映を含む。鏡映軸ではないすべり鏡映軸がある。すべり鏡映軸には必ずそれに平行な鏡映軸がある。 |
| pmg | 鏡映を含む。鏡映軸ではないすべり鏡映軸がある。鏡映軸ではないすべり鏡映軸にはそれに平行な鏡映軸がない。 |
- （C）90°回転を含む。
| p4 | 鏡映、すべり鏡映を含まない。 |
| p4m | 90°回転の中心を通る鏡映軸がある。 |
| p4g | 鏡映を含む。90°回転の中心を通る鏡映軸がない。 |
- （D）120°回転を含む。60°回転を含まない。
| p3 | 鏡映を含まない。 |
| p31m | 鏡映を含む。鏡映軸が通らない120°回転の中心がある。 |
| p3m1 | 鏡映を含む。どの120°回転の中心にもそれを通る鏡映軸がある。 |
- （E）60°回転を含む。
| p6 | 鏡映を含まない。 |
| p6m | 鏡映を含む。 |
これらについての作例を，
に示します．
参考：
平面充填入門
イントロダクション
ここでは，平面充填についての基本的な知識を紹介します．たくさんのWebサイトや書籍で紹介されているものですが，1箇所にまとまっている，簡単な，数式を使わないものはほとんどないようなので，まとめてみました．
参考Webサイト：
平面充填（Wikipedia日本語版）
Tessellation（Wikipedia 英語版）
List of Euclidean uniform tilings
分類のしかた
学者によってさまざまな分類方法があり，かなりの部分は重複しています．統一された見解というものはないようです．ここでは，大ざっぱに，「正多角形とそれ以外」「周期性と非周期性」という分類をしています．
- 正多角形に関する分類
- 大きさの同じ1種類の正多角形で構成（3種類＝ピュタゴラスの充填形）
- 正三角形
- 正方形
- 正六角形
- 大きさの同じ1種類の多角形で構成
- 任意の三角形
- 平行四辺形
- 平行六辺形（3組の対辺が平行で等しい六角形）
- 五角形（15種類あり，これ以上ないことが示されている）
- 複数種類の正多角形で構成（8種類＝アルキメデスの平面充填）
- [3, 3, 3, 3, 6]
- [3, 3, 3, 4, 4]
- [3, 3, 4, 3, 4]
- [3, 4, 6, 4]
- [3, 6, 3, 6]
- [3, 12, 12]
- [4, 6, 12]
- [4, 8, 8]
- 大きさの同じ1種類の正多角形で構成（3種類＝ピュタゴラスの充填形）
- 正多角形と、正多角形ではない+αの図形で構成
- 正多角形を使わない，特殊な充填形
- 周期性を持つか？
- 周期性
- 非周期性
正多角形とそれを使ったバリエーション
サブグリッドともよばれる，正多角形と、そのバリエーションの代表的な24種類を紹介します．これらは，正多角形を使った平面充填のほんの一部にすぎません．
充填できる＝角同士がぴったり合う＝足して360°になる，という視点から眺めてみましょう．
作例
＝アルキメデスの充填形、[3,6,3,6]
＝アルキメデスの充填形、[3,12,12]
＝アルキメデスの充填形、[3,4,6,4]
＝アルキメデスの充填形、[4,6,12]
＝アルキメデスの充填形、[4,8,8]
